テニスと心理学の架け橋 心理学のテニスへの応用を考える…よりもストリングのことを考えているかも

　ボールを目で追うこと・見ること①の続きです。

　随従運動の眼球運動の速さを30°/sまでと仮定した場合、「ボールを目で追う」ことができるのはテニスにおいてはどれくらいの速さのボールなのか、についてです。ケース１とケース２の分けて書きます。



ケース１

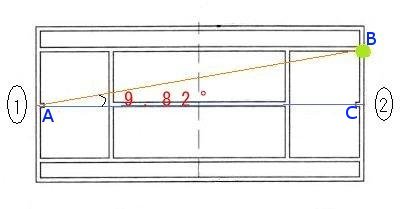
「１」という選手と「２」という選手がベースライン中央にいるとします。「１」の選手がボールを打つ人、「２」の選手がボールを見る人です。「１」はベースライン中央（A)からベースラインのサイドぎりぎり（B)に打ったとします。このケースにおいて、「２」の人はどれくらいの速さのボールを目で追うことができるのか、つまり30°/sの眼球運動で見ることができるボールの時速はいくらかを計算します。
　ABの長さは約24.11m、ACの長さは23.77m、BCの長さは4.114m、BACの角度は約9.82°になります。これらの値から計算しますが、過程は省略します。
　30°/sの眼球運動で見ることができるボールの時速は、およそ「32.73km/h」です。どう感じるでしょうか？かなり遅いと感じるのではないかと思います。計算ミスはたぶんない…はず。



ケース２

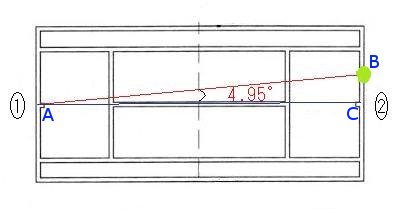
　ケース１はベースライン上のサイドラインぎりぎりのところでしたが、それではきついんじゃない？という自分自身の声にこたえるために（？）、ケース２を設定しました。図を見ればわかりますが、打球はベースライン中央とサイドの中間に落下した場合です。
　ABの長さは約23.85m、ACの長さは23.77m、BCの長さは2.057m、BACの角度は約4.95°になります。
　ケース１と同様に計算すると、30°/sの眼球運動で見ることができるボールの時速は、およそ「52.04km/h」です。ケース１とはかなり異なる値ですが、だいぶ遅いのではないかと思います。



　ケース１、２の総括ですが、その前に。この計算で考慮できないことが２点あります。１つは、我々の首の動きが考慮に入れられていない点です。眼球運動の実質の速さは、眼球運動の速度＋首（顔）の動く速度です。もっと速い打球にも目で追えるんじゃないの？という反論が可能な点です。
　もう１つは、ボールの上下の動きを計算に入れることができない点です。その中でも、とりわけ角度の変化が激しいバウンドを考慮できません。エッグボールでしたらバウンドせずとも角度の変化は相当だと思います。もっと遅い打球にしか目で追えないんじゃないの？という反論が可能な点です。
　この２つの点によって互いが相殺されるという生暖かい目で、僕の考察を見てみてください(；・∀・)長くなったので、考察は次回です。

（ボールの上下の動きもどうにか計算に入れられないかと考えました。そのために、実際にボールの動きを動画で撮影したりしましたが結局無理でした。撮影に協力してくれたSさん、ありがとうございました。）

ボールを目で追うこと・見ること③へ続く。